Introduction
这篇文章是语义分割任务中,首次端到端训练FCN用于逐像素预测,并且采用监督学习和预训练模型的。语义分割任务在语义性和位置之间有一些矛盾:全局信息解决是什么的问题,局部信息解决在哪里的问题。深度特征的层级结构在局部到全局的金字塔上共同编码了位置和语义信息。这篇文章定义了一种跨层连接组合深的,粗略的层上的语义信息和浅的,精细的层上的外观信息。
Fully convolutional networks
卷积网络因为全连接层或者全局池化层具有平移不变性,Mask R-CNN中也提到过:分类网络需要平移不变性,因为目标在任何位置,不应该影响对它的预测。但是对于检测或者分割任务而言,则需要平移同变性,因为目标位置的移动必须使得输出也相应改变。全卷积网络就具有平移同变性,这就非常适合分割任务。但是卷积网络输出的特征图分辨率是随着层数的加深越来越低的,这对分割任务是不利的,因为分割需要对图像边缘的像素进行精细地分类。
总之,对于传统的分类网络,运用到分割任务中,需要解决两个问题:
- 替换全连接层为卷积层,从而得到平移同变性的网络
- 需要将低分辨率的输出特征图恢复到原始图像尺寸,即上采样,从而得到更加精细的结果
Adapting classifiers for dense prediction
典型的识别网络比如LeNet,AlexNet等,它们的全连接层具有固定的维度并且丢弃了空间坐标信息。但其实这些全连接层可以被看做是卷积核覆盖了整个输入区域的卷积。下图是全连接转换为卷积层的过程,使得分类网络输出一个热点图(heatmap)。其实就是把4096-d的特征转换为1x1x4096的tensor。
具体实现的方式是:
对于AlexNet,第一个全连接层的输入是7x7x512的,原始网络后面是4096个单元的全连接层,只需将其改为:使用4096个7x7x512的卷积核,就可以得到1x1x4096的输出,后面也是使用与输入尺寸相同的卷积核,就可以把所有全连接层替换为卷积层了。
输出的特征图与原始网络的输出是等价的,但是参数量会更少。另外将网络转换为全卷积网络后,输入的图像就可以是任意尺寸的。因为原始网络需要固定输入主要是因为全连接层是固定维度的,它必须接受固定维度的输入。
Upsampling is backwards strided convolution
随着网络层数加深,特征图分辨率会越来越小(粗略)。而分割任务需要对应到原始图像尺寸,得到每个像素的类别,为了将特征图恢复到原始图像的分辨率,FCN使用了上采样。加入对于原始图像, 经过逐层卷积后,图像缩小了32倍,那么对于最后一层的输出,就需要32倍的上采样。
上采样的方式有两种:一是插值;二是反卷积。使用反卷积可以进行端到端的学习,相对于双线性插值来说,反卷积加激活函数可以学习到非线性的上采样。所以文中使用了反卷积做上采样,另外设计了跨层连接。不同的分辨率预测的精细程度是不同的,以下图中8x采样的预测特征图来看,它包含了3部分:conv7进行4x上采样+pool4进行2x上采样+pool3。作者对比了32倍,16倍以及8倍上采样的预测结果:
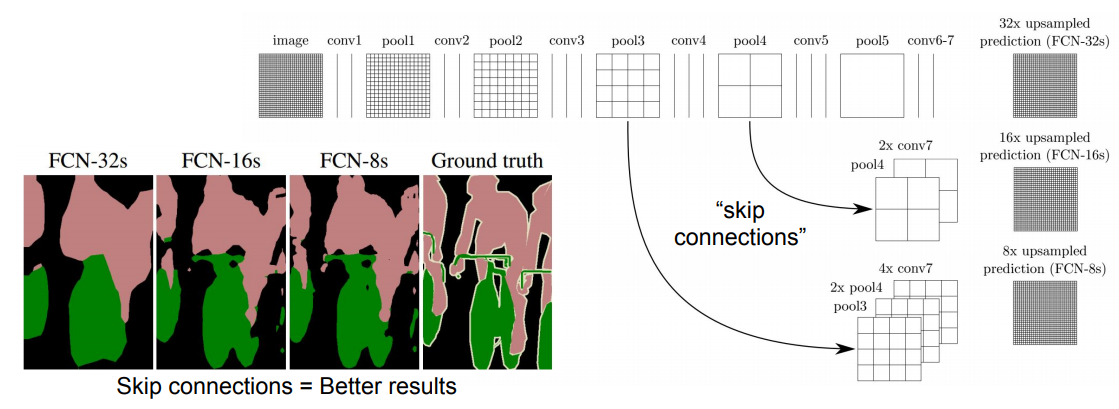
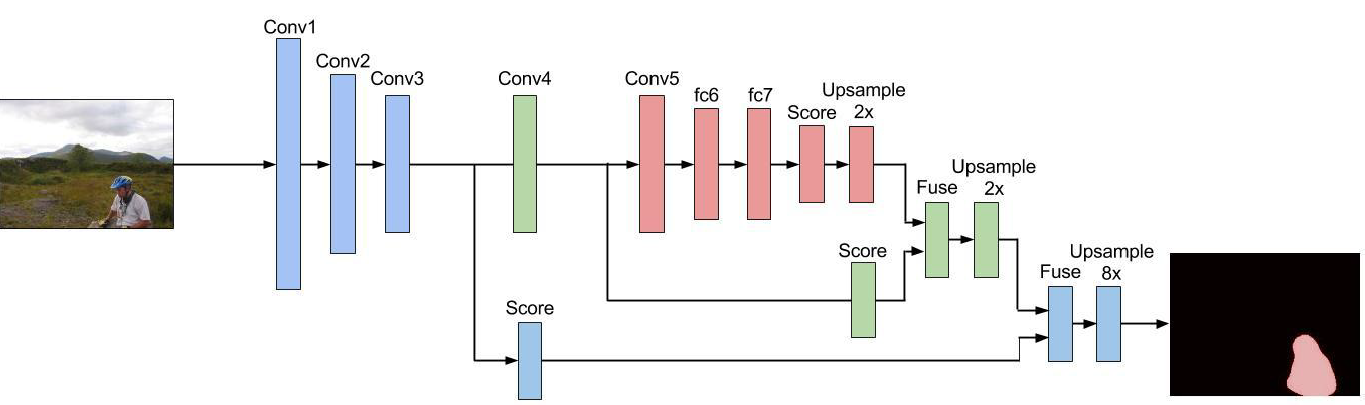
跨层结构具体如下图,如文中所说,它融合了深层较强的语义信息和浅层较精细的局部信息,是一种全局信息和局部信息的组合,即“Combining what and where”,达到对预测结果的精修。
Learnable Upsampling: “Deconvolution”
Deconvolution并不是一个非常准确的表达,比较正确的表达应该是转置卷积(convolution transpose )。
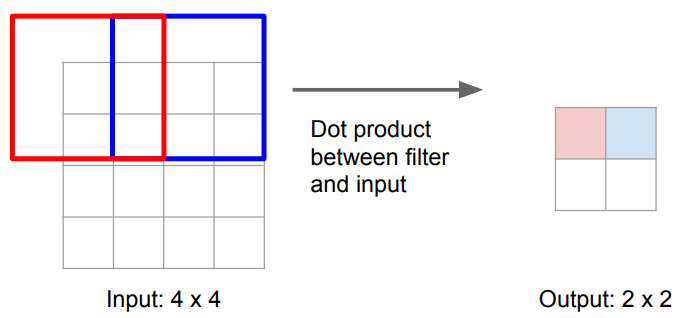
下面看一个卷积过程,输入经过stride为2,pad为1,size为3x3的卷积核,得到2x2的输出:
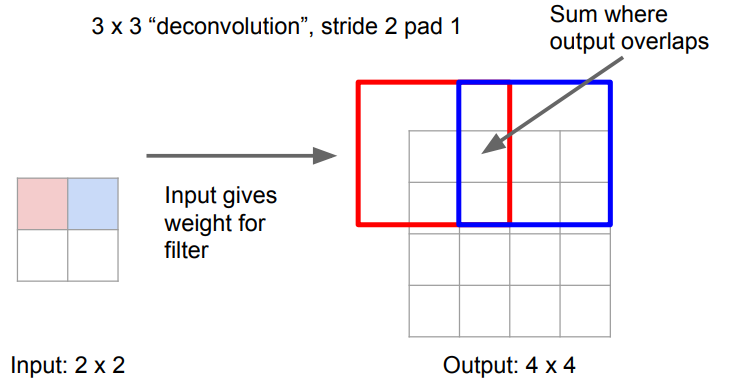
对于卷积的逆过程,输入是2x2,输出为4x4,要进行2倍上采样:
卷积层的前向传播过程,就等同于转置卷积的反向传播过程;卷积层的反向传播过程,就等同于转置卷积的前向传播过程。
简评
这篇文章实现了端到端的语义分割,“pixels in, pixels out”。给一张$W \times H$的输入图像,网络最终能输出$W \times H \times C$的预测,其中$C$代表了类别数。所以每一个像素点都可以被分类到一个类别,给语义分割任务提供了一个很好的思路。最终使用8x上采样的特征图能达到还不错的分割结果,但是多层特征图的融合,其实只是将全局和局部信息组合使用,对于结果有一定的精修作用。在这篇文章之后,有一篇对称反卷积网络,个人感觉,对称结构应该可以更好的解码,有待学习。