这篇文章是
CVPR2015上的文章,提出了FaceNet直接学习人脸图像到一个紧凑的欧氏空间的映射,空间距离直接对应于面部相似度的测量。主要的创新点就是提出使用triplet loss,并且得到的是128维的特征。在LFW数据集上达到了99.63%的准确率,在YouTube Faces DB达到了95.12%的准确率。
Introduction
这篇文章设计了一个统一的系统,用来做人脸验证和人脸识别,以及聚类。
- 人脸验证(
face verification):是不是同一个人?一对一 - 人脸识别(
face recognition):是哪一个人?一对多 - 人脸聚类(
face clustering):在这些人脸中寻找一类人,比如血亲,双胞胎等
提出使用深度卷积神经网络学习人脸到欧式空间的映射,以使欧式空间中的L2平方距离可以直接对应于人脸相似度:在欧氏空间中同一个人的面部特征有着较小的距离,而不同的人的面部特征有着较大的距离。

上图展示了光照和角度变换下,图像对之间的距离。距离为0的话意味着人脸是相同的,而距离为4.0意味着是两个不同的身份。纵向是不同人的图像对,横向是同一个人的图像对,可以看到,取1.1的阈值,可以正确地分类是否为同一个人。
这样解决前面的三种任务就很直接了:人脸验证就只涉及两个图片之间距离的阈值;人脸识别变成了一个K-NN问题;人脸聚类可以通过现有的(off-the-shelf)技术,比如k-means或者凝聚聚类(agglomerative clustering)。
先前的基于深度网络的人脸识别使用一个分类层在已知人脸身份的训练集上进行学习,然后使用中间的瓶颈层(bottleneck layer)作为特征表达去泛化识别性能。这些方法不够直接也不够高效,因为要寄希望于bottleneck layer,让特征表达对新的人脸有很好的泛化性能,并且使用bottleneck layer,特征表达的尺寸也有1000s的维度。
FaceNet使用基于LMNN的三元组损失(triplet-based loss)直接训练出紧凑的128-D的特征。三元组包括:两个匹配的人脸缩略图、一个不匹配的人脸缩略图。loss的目标就是通过距离间隔(margin)将正样本对和负样本分离开。
Method
对比两种核心的网络结构:一个是Visualizing and Understanding
Convolutional Networks这篇文章中的网络,另一个是Inception。FaceNet的结构如图。包含一个batch input layer和一个深度CNN,而后是L2标准化(L2 Normalization),产生所谓的Face Embedding,这个奇怪的词汇face Embedding就是人脸图像到欧氏空间的映射,前面做的就是特征提取。训练过程中最后还有一个triplet loss。

Triplet Loss
这种embedding使用$f(x) \in R^d$表达,将输入图像$x$嵌入到$d$维的欧式空间中。此外,这里限制它在$d$维超球面,即$||f(x)||_2 = 1$。
- 在该空间内,要确保对于某个特定的人,他的
anchor图像$x_i^a$与所有其他的正样本$x_i^p$距离近,与任何负样本$x_i^n$距离远。即类内距离加上间隔小于类间距离。表示为:$$||f(x_i^a) - f(x_i^p)||^2_2 + \alpha < ||f(x_i^a) - f(x_i^n)||^2_2~~~~ \forall(f(x_i^a), f(x_i^p), f(x_i^n)) \in \tau$$
$\alpha$是用在正负样本对之间的间隔margin。不仅要使anchor与正样本之间的距离小于它和负样本之间的距离,而且要小到某种程度。(SVM中margin不也是这个作用?)。$\tau$是训练集中所有可能的三元组(triplet),共有$N$组。 - 损失定义为:$$L = \sum_i^N \left[ ||f(x_i^a) - f(x_i^p)||^2_2 - ||f(x_i^a) - f(x_i^n)||-2^2 + \alpha \right]_+$$
这个式子右下角有个$+$号,表示:对于每一组三元组,如果不满足目标不等式时会产生一个为正数的差,损失值就是这个差值,而如果满足目标不等式,损失值会小于0,就取损失值为0。就是对于不满足条件的三元组,进行优化,满足的就不管了。所以目标就是最小化这个损失,让anchor靠近postive而远离negtative,如下图: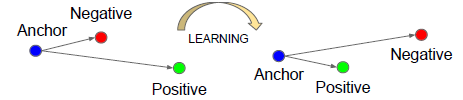
Triplet Selection
如何选择三元组是训练的关键。太简单的三元组对训练网络没有帮助,只有那些比较难的三元组才会改善网络性能,加速收敛。所以关键的是选择出那些违背上面不等式的三元组。
- 给定$x_i^a$,要选择的难的正样本需要使
anchor和正样本之间的距离大
$$argmax_{x_i^p}||f(x_i^a) - f(x_i^p)||_2^2 $$ - 相似地,选择难的负样本要使
anchor和负样本之间的距离小
$$argmin_{x_i^n}||f(x_i^a) - f(x_i^n)||_2^2$$
文章中说选择最难的负样本会导致在训练早期得到局部最优解,因此不选择最难的负样本,而是选择较难的(semi-hard),也就是说负样本比正样本远离anchor,同时anchor-negtative的距离接近anchor-postive的距离。
生成三元组时,每个mini-batch中对每个身份选择40个人脸,并且随机采样一些负样本人脸。文中mini-batch是1800个样本。
训练时使用SGD和AdaGrad优化。学习率开始设为0.05,$\alpha$设为0.02。好吧,模型随机初始化,以超强的自信心在CPU集群上丧心病狂地训练了1000~2000小时,也就是41~83天。训练了500个小时后,loss和准确率的变化才减慢。